The Science

Source: Glenn Tattersall

What does an thermal image tell us?

An infrared camera is able to, using the radiation emitted by objects, calculate the surface temperature of everything in the frame. It's important to note that it can only observe surface temperatures, and not the core temperatures of, for example, large mammals. The temperature is shown on the image through the color palette.


The thermal image on the left depicts a lizard basking. Lizards bask as a way to increase their body temperature above that of the surrounding air temperature. We note how effective basking is, as the lizard's temperaure is around 35˚C, while the rock is around 25˚C. If the heat isn't coming from the rock, where's it coming from? Generally, basking increases the amount of heat coming from solar radiation and decreases heat loss from convection (wind).

Thermal Imaging in Physiology

We highlight examples of how thermal images have been used to study organismal physiology and its dependence on environmental conditions.

Thermal imaging has been used to study issues including temperature preferences and the influence of aggregation on thermoregulation. An thermal imaging study of sea star thermoregulation (Pincebourde et al. 2009) found they accumulate water at high-tide to slow their temperature change when exposed at low-tide. Thermal imaging has also been used to study whether incubation temperatures affect gecko upper and lower preferred temperatures (it does, Blumberg et al. 2002). Another application of thermal imaging finds temperature differences among appendages: bat wings, due to their large surface area, remain near ambient temperatures while bat body temperature rises during flight (Lancaster et al. 1997).


Assessing thermal preference in lizards within a thermal gradient (Khan et al. 2010).


Thermal imaging can also be used to study evaporative cooling (cooling from a moist surface). Humans are well acquainted with evaporative cooling, which happens while sweating. Reptiles have been found to regulate their breathing patterns to control their head and brain temperatures through evaporative cooling (Tattersall et al. 2006a).


A frog with moist skin (A) being exposed to a gust of air and (B) minutes later returning to normal temperatures after avaportative cooling has ceased (Tattersall, 2016; Tattersall et al., 2006b; Tattersall et al., 2004).


One application of thermal imaging for endotherms is estimating the effects of insulation (typically fur and feathers). An endotherm with a thick insulating cover should exhibit cooler surface temperatures which are closer to ambient temperature. Prior to shearing insulating fiber, surface temperatures of a llama's normal 15cm thick pelage was ~26 °C, compared to surface temperatures of ~33 °C when the fiber was clipped to 1 cm thick (Gerken, 1997).


Surface temperature of the pelage of endotherms reveals differences in insulation. Panel A is a thermal image of two dogs (Australian Shepherds) outside at 0 °C. The left dog has a congenital lack of undercoat fur and has surface temperatures ~4 °C warmer than the dog on the right with a thick insulating coat. The horse in panel B has had fur clipped in places, revealing surface temperatures that are higher and approaching body temperature.


Thermal imaging has vast potential in the field of physiology. We hope to encourage greater use of Thermal imaging to see how organisms experience their thermal environment.

How is heat transferred?



Radiation

A heat transfer between two substances that are not in contact. The largest source of heat in most cases is the absorption of solar radiation. Animals radiate energy at a rate proportional to their body temperature (thermal radiation).


Conduction

A heat transfer involving two objects in physical contact with each other. Organisms can alter rates of conduction by changing their amount of contact with surfaces.


Convection

A heat transfer between a solid and a liquid or a gas. Wind and water speeds influence how much heat organisms exchange with their environments via convection.


Evaporation

A loss of heat due to the liquid water changing into gaseous water. Evaporation occurs when a fraction of water molecules have sufficient heat energy to escape a liquid. Organisms are cooled by evaporation until an equilibrium is reached where the air supplies the amount of heat removed by the evaporating water.

Why use thermal imaging for thermal ecology?

#1: non-invasive and #2: non-contact

Thermal information can be assessed from a distance, without handling of organisms or surgical interventions. Surgery and handling often affect the temperature of an organism due to stress. Another benefit is the ability to capture thermal readings of the environment around an organism, allowing comparison of temperature differences. A disadvantage, however, of using thermal imaging is the inability to measure an organism's core temperature, as infrared imaging only allows readings of surface temperature. Application of IRT to animal physiology are thus limited to small ectotherms or must be paired with biosphysical models to estimate core body temperature.

Thermograms

A thermogram is simply an image, impression, or visual representation of a scene's temperature. It is the visual rendering of the energy emitted, transmitted, and reflected by an object and its environment. All objects emit electromagnectic radiation from the random collision of matter, termed "radiant flux." There is a strong positive relationship between an objects termpature and it's radiant flux, allowing accurate radiometers to estimate object temperature. This calculation, however, depends on the emissivity of the objects pictured.



Blackbodies and Radiation

An ideal blackbody is an object which absorbs all electromagnetic radiation at all wavelengths. It emits energy at a maximum potential rate per unit area and unit wavelength at any temperature. No real objects are true blackbodies, however this idealized object gives a baseline for comparisons. A blackbody's spectral radiance, I, at a given wavelength and temperature is calculated using Planck's Law (h is the Planck constant, k is the Boltzmann constant, and c is the speed of light):

.

This equation gives a resulting curvilinear relationship.



The peak occurs at a wavelength which we can use to solve for blackbody temperature using Wein's law (b is Wein's displacement constant):

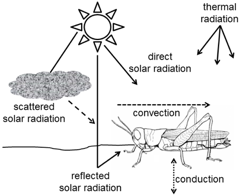
At a given wavelength, for biological surfaces, incoming radiation is either reflected or absorbed. An ideal blackbody, which by definition absorbs all incoming radiation, emits radiation equivalent to the amount of radiation absorbed.This is also means emittance and reflectance are inversely related, or as Kirschoff's radiation law is summarized: “good absorbers are good emitters and good reflectors are poor emitters.” A blackbody represents the upper limit of radiation emitted.

Stefan-Boltzmann's Law shows the relationship between the absolute temperature of the blackbody (T) and the blackbody's radiant flux (Mb) as (given sigma as the Stefan-Boltzmann constant and A as the surface area):

Now that we have data on blackbodies, the upper limit of emitted radiation, we can factor in emissivity, which is the ratio of the body's radiant flux to that of a blackbody at the same temperature:

Emissivity is assumed for biological tissues as > 0.95.

Since natural object do not behave exactly as blackbodies, background reflectance must be factored in. Since reflectance = 1 - emittance, the absolute temperature (often air temperature) has a maximum error of 1 - emittance, or about 5%. Atmospheric conditions (humidity) and distance from the imaged object also impact the radiant energy detected. The longer the distance, the greater the atmospheric interference due to the absorption of radiant energy by the water moledules. If a window is between the sensor and the object, energy may be lost in transmission through the window, requiring estimation of tranmission levels of the window materials and discouraging window use if possible. Finally, camera specs and stability are factored into calibration of the signal based on the camera used.



Signal to temperature



The object's signal is first separated from the whole signal (in this case, no transmission window):

This showcases the need for accurate information on the environmental conditions the image was taken in. The calibration of the camera empirically fits coefficients R, B, and F, and along with the signal s can solve for temperature.


->